
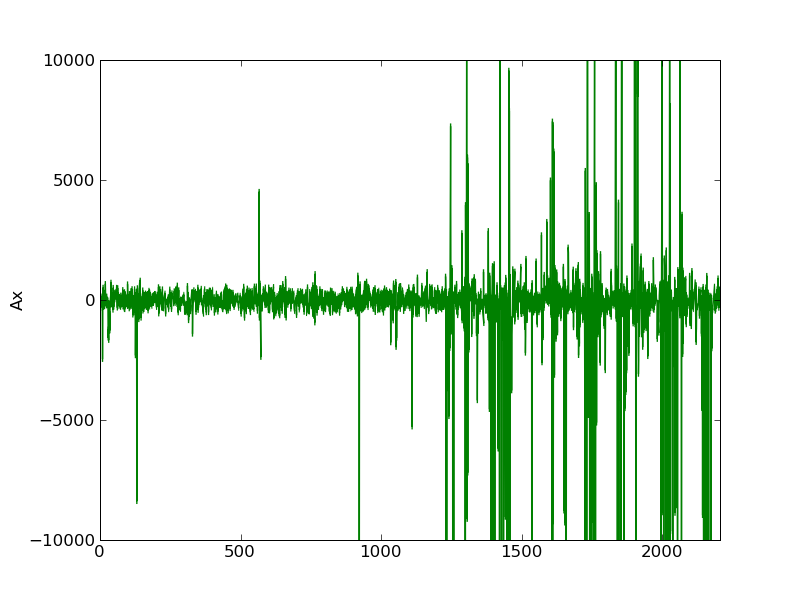
The faster Gauss Jacobi implementation is not only significantly faster than every other implementation, but it does not seem to increase with array size like the other methods. N Gauss-Jacobi Gauss-Jacobi Fast Gauss Seidel SOR - w=1.5

I ran randomized tests on 100 NxN Diagonally dominant matrices for each N = 4.20 to get an average number of iterations until convergence. Both of these were implemented in a similar way to my original, slow Gauss-Jacobi method. I've implemented two other methods, the Gauss-Seidel Method and the SOR method. What makes the second implementation so much faster than the first? The first implementation takes 37 iterations to converge with an error of 1e-8 while the second implementation takes only 7 iterations to converge. def GaussJacobi(A, b, x, x_solution, tol): The second implementation is based on this article. X_new = np.zeros(N, dtype=np.double) #x(k+1) The first implementation is what I originally came up with import numpy as npĭef GaussJacobi(A, b, x, x_solution, tol): 13.3.When implementing the Gauss Jacobi algorithm in python I found that two different implementations take a significantly different number of iterations to converge. We therefore need another way of handling this type of problems. But beware, on a fairly recent Macbook Pro with \(16\) Gb of memory, the computation literally stalled when the number of grid points in both direction was multiplied by \(2\). If you want to increase the precision, you need to refine the grid. We have collected some conclusive evidence that our procedure worked very nicely! Let’s use it to assess the precision of our solution:

\ = pvec p = 0 p = 0 p = 0 p = 0 # Compute the exact solution p_e = p_exact_2d ( X, Y )Īt the beginning of the notebook, we have imported the l2_diff function from our module file module.py. Consider as an example the Poisson equation in three dimensions: This is especially true when solving multi-dimensional problems.
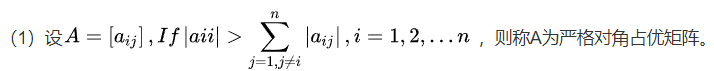
However, for very large systems, matrix inversion becomes an expensive operation in terms of computational time and memory. When the size of the matrix is not too large, one can rely on efficient direct solvers. Their implementation is a bit more complicated in the sense that they require the inversion of a matrix. In the previous chapter we have discussed how to discretize two examples of partial differential equations: the one dimensional first order wave equation and the heat equation.įor the heat equation, the stability criteria requires a strong restriction on the time step and implicit methods offer a significant reduction in computational cost compared to explicit methods. insert ( 0, './modules' ) # Function to compute an error in L2 norm from norms import l2_diff % matplotlib inline Import numpy as np import matplotlib.pyplot as plt from scipy.sparse import diags import sys sys.


 0 kommentar(er)
0 kommentar(er)
